ML History : Linear Regression
선형 회귀의 역사
1800년대에 행성의 이동, 완두콩의 크기 예측 위해 발명
수기 계산을 할때 고안되었지만 거대한 데이터셋에서도 잘 동작
선형 회귀 알고리즘
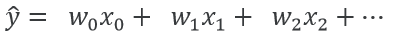
→ hypothesis equation
각 feature의 값(x)에 각 가중치(w)를 곱한 값의 합이 선형 회귀 모델이 예측하고자 하는 값이 된다.
가중치 적절히 설정해 예측값이 좋은지 나쁜지 검증 방법
→ 손실측정함수(loss function)
ex) regression problem의 MSE
: 실제 값과 예측한 값의 차이의 평균이 최소화 되는 지점 찾아야 함
선형 회귀에서 손실 값 최소화 할 수 있는 가중치 찾는 공식 존재

단점
→ 시간복잡도 O(N^3)
→ 현실에는 중복되거나 거의 중복되는 값을 가지는 데이터 많음
경사하강 최적화 알고리즘
- 시간, 메모리 자원을 덜 사용
- 일반화에 조금 더 유리
- 대부분의 문제에 적용 가능
경사하강법
경사 하강법 적용을 위해 가중치 파라미터에 대한 손실값 공간을 보면 hill / valley가 나타난다.
손실이 최소가 되는 지점(가장 낮은 valley)이 모델이 도달해야 하는 지점인데, 이 때 하강 방향, 경사의 정도를 손실 측정함수로 구한다.
이를 통해 구해진 정보를 가지고 이동하는 사이즈를 learning rate라고 하고 이는 학습 전 설정되는 hyper-parameter의 한 종류이다.
※ learning rate가 큰 경우 : 경사하강법이 오히려 더 큰 손실점으로 이동하게될 수도 있음
learning rate가 작은 경우 : 경사하강법이 너무 오래걸리게 됨